CKtrace's Devlog
[통계] - 공분산 & 상관 계수 (feat. 산점도) 본문
산점도(Scatter plot)
공분산과 상관계수를 알기 위해서는 산점도란 무엇인지 우선 알아야 합니다.
산점도(Scatter) 연속형 변수 두 개 간의 관계를 보기 위해서 평면에 점을 찍어 만든 통계 그래프입니다.

산점도 그래프를 보아 알 수 있듯이 점들은 두 변수 x, y 순서쌍 자료 값에 맞게 찍힙니다.
공분산(Covariance)
공분산(Covariance)은 두 변수 간에 직선 관계가 어느 정도인지를 나타내 주는 통계 값입니다.
공분산은 위에서 설명한 산점도를 통해서 두 변수 간에 관계의 존재 여부를 시각적으로 확인할 수 있습니다.
평균 순서쌍 값인 (x, y)를 기준으로 분포하는 형태에 따라 아래의 두 가지 관계로 분류할 수 있습니다.
- 평균 순서쌍 값인 (x, y)를 중심으로 1 사분면과 3 사분면에 자료가 많고 길게 분표 할 경우 -> 양의 관계
- 평균 순서쌍 값인 (x, y)를 중심으로 2 사분면과 4 사분면에 자료가 많고 길게 분표 할 경우 -> 음의 관계
양의 관계일 경우 아래의 그래프와 같이 산점도가 양의 기울기를 가집니다.

음의 관계일 경우 아래의 그래프와 같이 산점도가 음의 기울기를 가집니다.

이를 통해 평균 순서쌍 값인 (x, y)로부터 멀어질수록 직선 관계가 분명해짐을 알 수 있습니다!
표본 공분산(Sample Covariance)의 일반식과 간편식


여기까지 보신 분들 중에 아래와 같은 궁금증을 갖게 되신 분들이 계실 겁니다.
c > 0일 때는 양의 관계, c < 0일 때는 음의 관계
그렇다면 c = 0이거나 0에 근사할 때는?
그래서 바로 밑에서 c = 0이거나 0에 근사할 때 산점도를 알아보려고 합니다!
Scatter plot when c ≈ 0
직선 관계가 없는 c≈0일 때 산점도의 두 가지 어떤 형태를 보여드리도록 하겠습니다.
첫 번째는 c≈0이고, 4 사분면이 모두 비슷하게 분포한 산점도입니다.
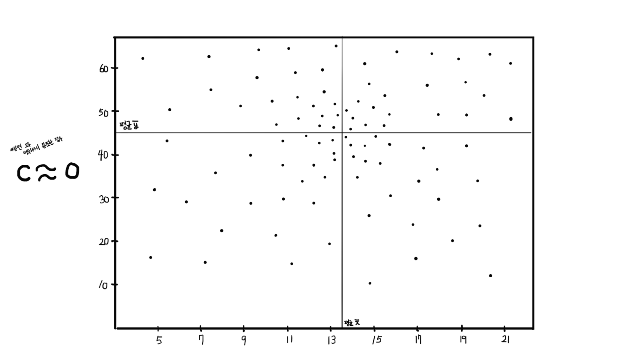
두 번째는 c≈0이고, 1 사분면과 2 사분면이 비슷하게 분포하고, 3 사분면과 4 사분면이 비슷하게 분포한 산점도입니다.
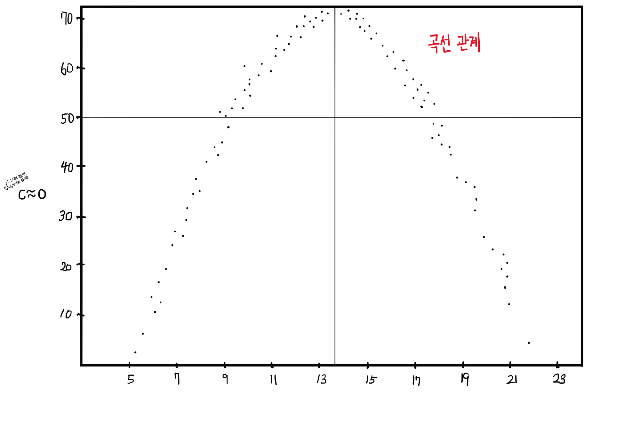
상관 계수 (Coefficient of Correlation)
상관 계수(Coefficient of Correlation)는 공분산의 문제점을 보완해주는 값입니다.
문제점은 바로 공분산이 측정 단위에 영향을 많이 받아서 공분산 그 자체로 선형 관계의 정도는 알 수 없다는 것입니다.
한마디로, 양수인지 음수인지는 알 수 있지만 양수 값끼리, 음수 값끼리의 값 비교는 불가하다는 거죠...
상관 계수에는 피어슨 상관계수, 켄달 상관계수 등이 존재하지만 저희가 알아볼 상관 계수는 피어슨 상관 계수입니다.
왜냐하면 상관 계수라고 하면 대부분 피어슨 상관 계수를 의미하기 때문입니다.
글이 더 길어질 것 같아 피어슨 상관 계수 내용은 다음 포스팅에서 찾아뵙도록 하겠습니다.
지금까지 공분산과 상관 계수에 관한 내용 잘 읽어주셔서 감사합니다.
이어지는 피어슨 상관 계수 내용도 잘 읽어주시면 감사하겠습니다!
'Statistics' 카테고리의 다른 글
| [통계] - 정규 분포와 표준 정규 분포 (0) | 2021.12.31 |
|---|---|
| [통계] - 피어슨 상관 계수 (0) | 2021.12.30 |
| [통계] - 포아송 분포 (feat. 이항 분포) (0) | 2021.12.28 |
| [통계] - 몬티홀 문제 (Key : 조건부 확률) (0) | 2021.12.25 |
| [통계] - 분포의 형태 (왜도 & 첨도) (0) | 2021.12.24 |




